
ForkJoinPool jest specyficzną pulą, która została dodana w Javie 7, jednakże na dobre zaczęto jej używać w Javie 8. Pula ta służy do realizacji zadań, które da się podzielić. Do podziału problemów stosuje ona algorytm dziel i zwyciężaj, a te podzielone zadania przydzielane są dzięki wykorzystaniu algorytmu Work-Stealing. Jest to bardzo ciekawa pula, ponieważ jest współdzielona przez cały proces uruchomiony na JVM.
ForkJoinPool
Jeśli kiedyś zdarzyło wam się wywołać metodę .parallel() na strumieniu, uruchamiana była ona na puli ForkJoinPool. Jest to pula, która od Javy 8 wykorzystywana jest jako domyślna pula wątków. Realizuje ona zadania, które da się podzielić. Jak napisałem we wstępie pula ta wykorzystuje dwa algorytmy dziel i zwyciężaj oraz Work-Stealing.
Dziel i zwyciężaj
ForkJoinPool korzysta z algorytmu dziel i zwyciężaj. Jest to bardzo proste podejście, w którym dzielimy pracę na mniejsze podzadania:
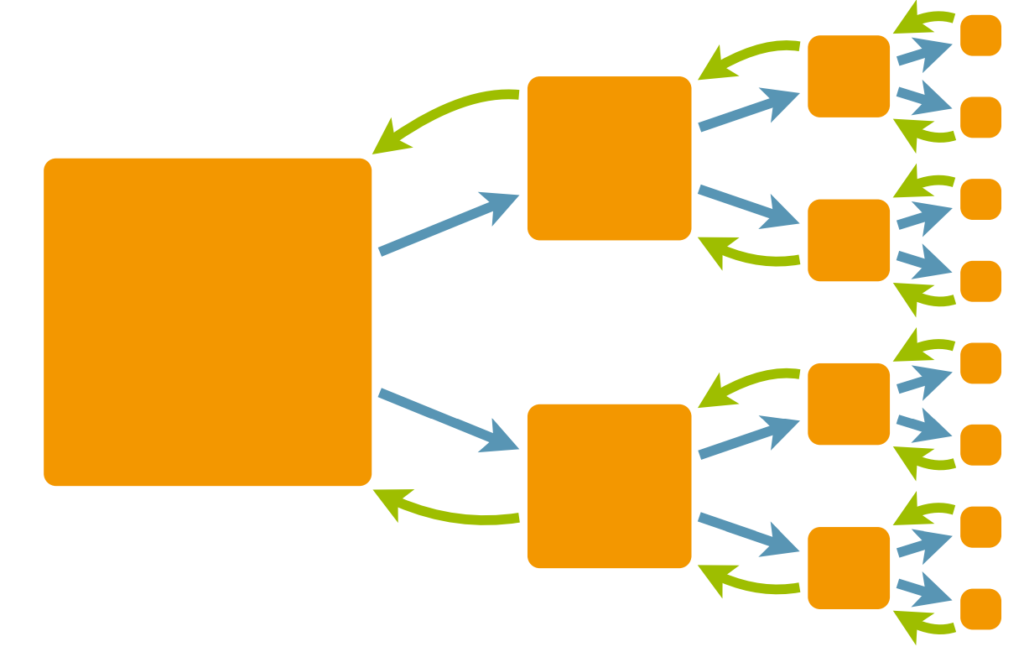
W kontekście tej puli, każdy podział nazwywany jest Fork’iem (niebieska strzałka), natomiast zwrócenie wyniku z podzadania Join’em (zielona strzałka).
Work-Stealing
Jeśli mamy podzielone zadania, trafiają one na kolejkę. Teraz obsługą tych zadań zajmuje się algorytm Work-Stealing, który przydziela zadania wątkom aktualnie bezrobotnym. Kradną więc one pracę innym wątkom:

Wielkość
Pulę tę możemy tworzyć sami poprzez:
ForkJoinPool pool = new ForkJoinPool(parallelism);
gdzie:
- parallelism – ilość wątków
Jeśli natomiast korzystamy ze współdzielonej puli, tak zwanej “common pool”, to ilość dostępnych wątków wyliczana jest według wzoru:
Runtime.getRuntime().availableProcessors() - 1
Dostępna jest ona pod statyczną metodą:
ForkJoinPool commonPool = ForkJoinPool.commonPool();
Zadania
Aby stworzyć zadanie, które da się podzielić, należy wykorzystać klasę RecursiveTask, która zwraca wynik lub RecursiveAction jeśli wynik nas nie interesuje:
/**
* Task which return result
*/
class Task extends RecursiveTask<Integer> {
protected Integer compute() {
return null;
}
}
/**
* Task which do not return result
*/
class Task extends RecursiveAction {
protected void compute() {
}
}
Musimy także zaimplentować metodę compute, która odpowiedzialna jest za wykonanie logiki. Dla metody tej można określić pewien wzorzec :
Result solve(Problem problem) {
if (problem is small) {
directly solve problem
} else {
split problem into independent parts
fork new subtasks to solve each part
join all subtasks
compose result from subresults
}
}
Korzystając z ForkJoinPool zaimplementujemy teraz logikę odpowiedzialną za zsumowanie liczb w tablicy:
class Sum extends RecursiveTask<Long> {
private static final int THRESHOLD = 1_000;
private final int[] numbersToSum;
private int low;
private int high;
Sum(int[] numbersToSum) {
this.numbersToSum = numbersToSum;
this.high = numbersToSum.length - 1;
}
private Sum(int[] numbersToSum, int low, int high) {
this.numbersToSum = numbersToSum;
this.low = low;
this.high = high;
}
protected Long compute() {
if ((high - low) <= THRESHOLD) {
long sum = 0;
for (int i = low; i < high; i++) {
sum += numbersToSum[i];
}
return sum;
}
int mid = low + (high - low) / 2; //get middle index
Sum left = new Sum(numbersToSum, low, mid); //get first part
Sum right = new Sum(numbersToSum, mid, high); //get second part
left.fork(); //split job
long resultFromRight = right.compute(); //compute result
long resultFromLeft = left.join(); //wait for result
return resultFromRight + resultFromLeft;
}
}
Jeśli rozmiar podzadania (w naszym przypadku rozmiar tablicy) jest mniejszy niż próg, to wykonujemy zadanie sekwencyjnie. Próg to wartość, dla której warto dalej dzielić nasze zadanie (czyli wykonywać równolegle). W przeciwnym przypadku wyliczamy środkowy indeks (aby podzielić tablice na dwie podtablice) i tworzymy dwa podzadania left oraz right. Podzadania te otrzymują tę samą tablicę do sumowania, jednakże z mniejszą liczbą indeksów. Metoda fork() dzieli pracę, compute() wylicza wynik, a join() czeka na wynik operacji. Co ważne, nie ma żadnego “magicznego” sposobu na określenie wartości progu. Przed dobraniem odpowiedniego rozmiaru należy zmierzyć wyniki dla różnych wartości.
Uruchamiamy
Aby uruchomić nasze zadanie, należy utworzyć pulę wątków korzystając z klasy ForkJoinPool:
ForkJoinPool pool = new ForkJoinPool();
int[] ints = new Random()
.ints(0, 100)
.limit(1_000_000)
.toArray();
Long invoke = pool.invoke(new Sum(ints));
Kiedy warto?
Jeśli mamy zadanie, które da się podzielić na mniejsze podzadania, pula ForkJoinPool jest bardzo dobry wyborem.